...
Στο βιβλίο του πανεπιστημιακού, Θ. Μόδη (Θ.Μ.), «Προβλέψεις» (*), υποστηρίζεται ότι η πορεία κάθε ανθρώπου ως δημιουργικής μονάδας είναι περίπου προδιαγεγραμμένη και μπορεί να περιγραφεί, με μεγάλη ακρίβεια, με κατάλληλες μαθηματικές συναρτήσεις.
Από αυτές τις συναρτήσεις προκύπτει ότι μία σταθερή κάμψη στις δραστηριότητες και στην παραγωγικότητα κάθε ανθρώπου δηλώνει ότι αυτός δεν έχει πια τίποτα να προσφέρει και μοιραία οδηγείται στο θάνατο. Φέρνει δε ως παραδείγματα, μεταξύ άλλων, τον κορυφαίο συνθέτη W.A. Mozart (πέθανε το 1791 σε ηλικία 35 ετών, μάλλον από χρόνια νεφρική δυσλειτουργία, καθυστερημένη επίπτωση παιδικής ασθένειας), το διάσημο φυσικό Albert Einstein (πέθανε στα 76 χρόνια του το 1955) και τον επίσης διάσημο για τα έργα και την περιπετειώδη ζωή του συγγραφέα E. Hemingway (αυτοκτόνησε το 1961 σε ηλικία 62 ετών). Αυτό σημαίνει ότι και οι τρεις δημιουργοί πέθαναν «γέροι». Και ως προς τον Einstein θα μπορούσε να ισχυριστεί κάποιος καλόπιστα ότι στα 76 του ένας άνθρωπος της δεκαετίας του '50 πράγματι είναι γέρος ή ακόμα και για τον Hemingway, ότι έχει αρχίσει να γερνάει. Αλλά ο Mozart; Ήταν από πλευράς δημιουργικότητας, εμπνεύσεως και παραγωγικότητας ο Mozart στα 35 του «γέρος»;
Διατυπώνουμε εισαγωγικά τη θέση ότι ο Θ.Μ. δεν φαίνεται να έχει επιλέξει τα κατάλληλα παραδείγματα (Mozart, Hemingway και Einstein) για να τεκμηριώσει τη θεωρία του. Αν όμως αυτά τα παραδείγματα είναι τα καλύτερα δυνατά που βρήκε, τότε η θεωρία του πιθανόν να έχει μόνο στατιστική σημασία, να περιγράφει δηλαδή τη συμπεριφορά ευρύτερων ομάδων πληθυσμού, αλλά να μην επιτρέπεται να εξειδικευτούν τα συμπεράσματα σε συγκεκριμένα άτομα.
Αφήνουμε δε ανοικτά τα φιλοσοφικά προβλήματα που προκύπτουν από την περίπου μοιρολατρική αποδοχή μιας προκαθορισμένης πορείας ενός ανθρώπου, χωρίς την αποφασιστική σημασία στη ζωή μας του παράγοντα τύχη, χωρίς την ικανότητα για αλλαγή πορείας με προσωπική βούληση. Νομίζουμε ότι το Πανεπιστήμιο της «καθημερινής ζωής» δεν δικαιώνει τον Θ. Μ.
Μαθηματική περιγραφή
Η «σιγμοειδής» καμπύλη (σχήμα πάνω αριστερά, από την ομοιότητά της με το λατινικό γράμμα S) που εισάγει ο Θ.Μ. προκύπτει από την αθροιστική καταχώρηση γεγονότων (συνθέσεις, συγγραφή βιβλίων, δημοσίευση επιστημονικών μελετών κτλ.) με το χρόνο στον οριζόντιο άξονα. Αυτή η καμπύλη χαρακτηρίζεται από οριζόντια εφαπτομένη κατά την εκκίνηση, από μία περισσότερο ή λιγότερο ταχεία εκθετική ανάπτυξη και, τέλος, από προσέγγισή της σε μία ασυμπτωτική τιμή. Η προσέγγιση αυτή είναι απεριοδική (δηλαδή χωρίς ταλαντώσεις), όπως δείχνουν οι καμπύλες για τον Mozart και τον Hemingway. Προϋπόθεση βέβαια να επιδέχονται αυτή τη μαθηματικοποίηση οι δραστηριότητες κάθε ανθρώπου είναι να εκδηλώνονται μέσα σε «μόνιμη κατάσταση λειτουργίας». Αλλιώς θα είχαμε διαταραχές γύρω από τη θεωρητική τιμή της μόνιμης καταστάσεως.
(click)
Η πρώτη ένσταση από πλευράς μου είναι ότι, αυτή η μόνιμη κατάσταση λειτουργίας σπανίως αποκαθίσταται, γιατί ενσκήπτουν ανεξέλεγκτες εξωτερικές διαταραχές (ασθένειες, οικονομικές κρίσεις κτλ.), με αποτέλεσμα να προκαλείται αποσταθεροποίηση. Το εξεταζόμενο «σύστημα», αν επιβιώσει, θα αναγκαστεί να ξεκινήσει από την αρχή - αυτός είναι ο αέναος κύκλος της ζωής. 'Όλο το μυστικό της επιτυχίας είναι να αποφύγουμε ή να διαχειριστούμε σωστά τις «ανεξέλεγκτες εξωτερικές διαταραχές»... Σωστή διαχείριση δεν σημαίνει δε κατά μέτωπο σύγκρουση με το πρόβλημα, κάθε άλλο! Μπορεί να σημαίνει και αφομοίωση, ακόμα και αξιοποίηση της εξωγενούς διαταραχής, η οποία διαφορετικά θα μπορούσε να είναι καταστρεπτική.
Σε μία συνέντευξή του στο δημοσιογράφο Τάκη Μίχα (ΕΛΕΥΘΕΡΟΤΥΠΙΑ) αναφέρει ο Θ.Μ. ότι στην πορεία δεν είναι δυνατόν «να αλλάξουμε ζωή», όπως δεν είναι δυνατόν, λέει, να στρίψουμε δεξιά ή αριστερά όταν ένα όχημα τρέχει με μεγάλη ταχύτητα. Βεβαιότατα, μία στροφή 90o με ταχύτητα 120 km/h θα αποτελούσε καταστροφικό εγχείρημα. Με αυτούς τους όρους πράγματι δεν γίνεται να στρίψουμε σε ορθή γωνία! Αλλά, υπάρχουν και οι ανοικτές στροφές, υπάρχει και η επιβράδυνση του αυτοκινήτου που αντιστοιχούν σε χρονική κλιμάκωση δραστηριοτήτων στο παράδειγμα του Θ.Μ. Αυτή είναι η μαεστρία της σωστής διαχειρίσεως, αυτή είναι η «τέχνη της ζωής», η οποία δεν είναι εξασφαλισμένη και δεν αναγνωρίζεται σε κανένα άνθρωπο παρά μόνον απολογιστικά.
(click)
Τα παραδείγματα
Ως προς τα παραδείγματα που αναφέρονται στο βιβλίο του Θ.Μ., αφήνουμε καταρχάς ανοικτό το ερώτημα, κατά πόσον κορυφαίοι δημιουργοί με σύνθετη και εκρηκτική προσωπικότητα, όπως ο Mozart και ο Hemingway, είναι δυνατόν να «κλειστούν» σε μία ποσοτική αποτίμηση του έργου τους και αυτό να περιγραφεί με μαθηματικές εξισώσεις. Ας παραβλέψουμε επίσης ότι δεν είναι εύκολο να αποφασίσει κάποιος, τι σημαίνει «έργο» το οποίο θα συναθροίσει: μια όπερα και μια σονάτα μετράνε το ίδιο; Ο πίνακας Guernica του Picasso και κάποια προσωπογραφία του μετράνε ως ισότιμα; Κι αν όχι, πόσες καντάτες αντιστοιχούν σε μια συμφωνία και πόσα σκίτσα σε ένα τοπίο;
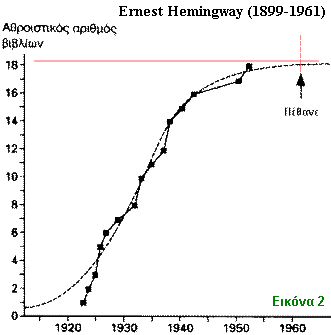
Το συμπέρασμα που μπρούμε να βγάλουμε προσωρινά είναι ότι οι καμπύλες που περιέχονται στο βιβλίο του Θ.Μ. και δείχνουν να συμπίπτουν περισσότερο ή λιγότερο τα σημεία πραγματικών γεγονότων με τα σημεία της ιδανικής σιγμοειδούς καμπύλης, δηλώνουν απλώς ότι το «σύστημα Mozart» (Εικόνα 1) προσομοιώνεται ως δυναμικό σύστημα αρκετά καλά, το «σύστημα Hemingway» (Εικόνα 2) απλώς ικανοποιητικά.
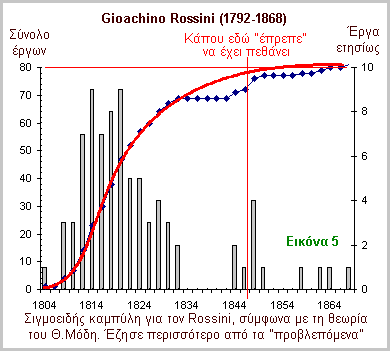
Στο παράδειγμα για τον Albert Einstein (Εικόνα 4) η προσομοίωση δεν είναι όμως επιτυχής. Πολύ λιγότερο θα δικαίωναν τη θεωρία του Θ.Μ. παραδείγματα, όπως ο Joseph Haydn και ο Gioacchino Rossini. O πρώτος έφτασε τα 77 χρόνια και τα έργα του, περί τις 2.000 αυτοτελή κομμάτια, είναι όλα γνωστά. Τα τελευταία έργα του γράφτηκαν το 1801, αλλά ο μεγάλος αυτός δημιουργός έζησε μέχρι το 1809. Ο δεύτερος έγραψε το τελευταίο σπουδαίο έργο του σε ηλικία 37 ετών. Έκτοτε και μέχρι τα 76 χρόνια του που πέθανε (1868), σχεδόν τίποτα. Κατά τη θεωρία του Θ.Μ., φαίνεται να έζησαν πέρα από τα αναμενόμενα και γι' αυτό αποσιωπούνται (δική μου Εικόνα 5).
Αλλά και σε άλλους τομείς δραστηριότητας υπάρχουν εντυπωσιακές δημιουργίες, ανεξάρτητα από την ηλικία. Ο Ελβετός Μαθηματικός Leonard Euler έγραψε τις καλύτερες μελέτες του σε ηλικία 70 ετών (έζησε 76 χρόνια), ο Goethe τελείωσε το έργο του Faust σε ηλικία 86 ετών, ο Πικάσο και ο Νταλί δημιούργησαν σημαντικά εικαστικά έργα στα τελευταία χρόνια της ζωής τους και οι διάσημοι μαέστροι Τοσκανίνι και Κάραγιαν άφησαν πίσω τους αξέχαστες ερμηνείες σε προχωρημένη ηλικία. Να υπενθυμίσουμε δε ότι και ο Αρχιμήδης ήταν ιδιαίτερα παραγωγικός λίγα χρόνια πριν δολοφονηθεί, σε ηλικία περίπου 75 ετών.
Ειδικότερα για τον Mozart φαίνεται από την καμπύλη, ότι η κυρτότητα έχει γίνει μεν ήδη αρνητική, η ασυμπτωτική τιμή της βρίσκεται όμως αρκετά υψηλότερα από το σημείο που δείχνει το έτος θανάτου (Εικόνα 3). Εκτιμούμε ότι η προσέγγισή της, σε αντιστοιχία και με τα άλλα παραδείγματα, θα απαιτούσε ακόμα περίπου 15, ίσως και 20 έτη. Με σωστή εφαρμογή της θεωρίας - όσο περίεργη κι αν διαβάζεται αυτή η διατύπωση - θα έπρεπε λοιπόν ο Mozart να πεθάνει ανάμεσα στα έτη 1806 και 1811, δηλαδή σε ηλικία 50-55 ετών! Αυτές οι ηλικίες πρέπει να θεωρηθούν υψηλές για εκείνη την εποχή που θέριζαν οι επιδημίες!
Στην καμπύλη του Hemingway, τώρα, έχει περίπου διαμορφωθεί η ασυμπτωτική τιμή (Εικόνα 2), αλλά είναι γνωστό ότι ο μακαρίτης πέθανε (αυτοκτόνησε) στα 62 του χρόνια, δηλαδή όχι πολύ μακριά από το μέσο όρο ζωής της εποχής του. Άρα το συμπέρασμα ότι ο Hemingway είχε περίπου ολοκληρώσει το έργο του, μπορεί να το διατυπώσει κάθε αμύητος και χωρίς αναλυτικά εργαλεία. Αυτά προκύπτουν από τις καμπύλες του Θ.Μ. και δεν φαίνεται να επιβεβαιώνουν τα συμπεράσματά του.
Όσον αφορά δε την καμπύλη για τον Einstein (Εικόνα 4), αυτή παρουσιάζει μία τελείως ιδιόμορφη συμπεριφορά και ο Θ.Μ. εκτιμά ότι τα «έργα» των τελευταίων ετών ζωής του Einstein ήταν επεξηγήσεις για παλαιότερες μελέτες του ή επιστολές κτλ., άρα αυτή η υπερδραστηριότητα του μεγάλου Φυσικού δεν έχει βαρύνουσα σημασία.
Αυτό είναι βέβαια μία εύκολη διέξοδος! Ποιος μπορεί να το κρίνει αυτό; Ποιος μπορεί να κρίνει αν τα μουσικά έργα σε κάποια φάση της ζωής ενός μεγάλου δημιουργού είναι ερμηνευτικά παλαιότερων προσπαθειών του; Και του Rossini τα έργα, μετά την τελευταία όπερα (1839) ήταν ασήμαντα θρησκευτικά έργα. Χωρίς αυτά η καμπύλη του Rossini θα ήταν επίπεδη ήδη από τη μέση του διαγράμματος περίπου. Ποιος μπορεί να κρίνει τη βαρύτητα του έργου KV 625 του Mozart, μία καντάτα για 2 τενόρους και ένα μπάσο, με συνοδεία ορχήστρας, το τελευταίο πριν από το Requiem, αν πρόκειται δηλαδή για μία αυθύπαρκτη δημιουργία ή είναι «ερμηνευτική», όχι με λόγια, αλλά με τα εργαλεία του μουσικού, για άλλα προγενέστερα έργα ή για το συνολικό έργο του συνθέτη; Γενικό συμπέρασμα από τα προαναφερόμενα είναι λοιπόν ότι, παρότι τα παραδείγματα του συγγραφέα είναι επιλεκτικά, ακόμα κι αυτά δεν καλύπτονται από τη θεωρία του.
(Στέλιος Φραγκόπουλος, Stelios Frangopoulos)
(*) Θ. Μόδη: Προβλέψεις, Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο 1996, σελ. 322
W.A.Mozart: Συμφωνία αρ. 39